Algorithms and Complexity

Institute of Computer Science — Department V

In Department V "Algorithms and Complexity", we focus on the design and theoretical analysis of algorithms. Our aim is to design improved algorithms in various application contexts and to develop a deeper understanding of algorithmic possibilities and limitations.

Efficient algorithms have been a driving force behind technical progress in recent decades. Without them, there would be no search engines that can search through large amounts of data in fractions of a second, no navigation systems and no secure communication on the Internet.

We conduct research on fundamental combinatorial issues in the field of algorithms and complexity as well as on algorithmic issues arising from other disciplines such as geodesy and economics.

Research Highlights

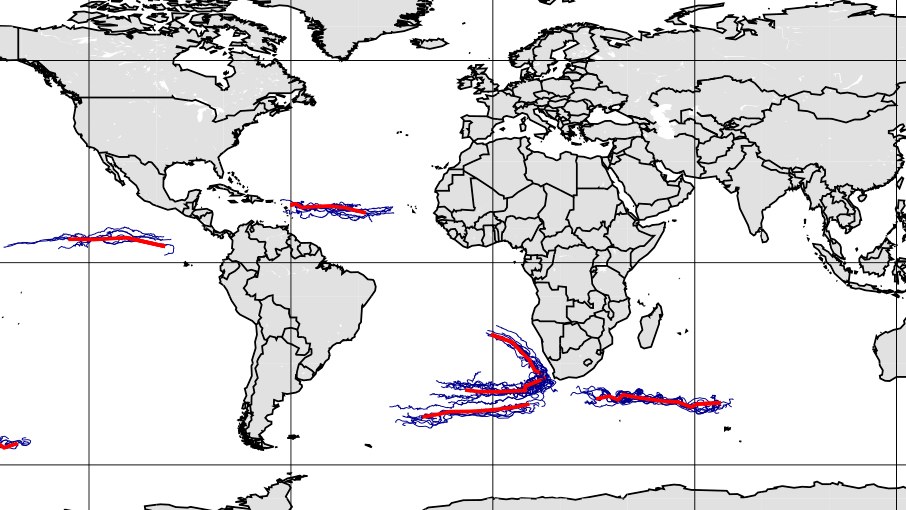
AI Research Group: Algorithmic Data Analysis for Geodesy (AlgoForGe)

As part of the research group, we develop new algorithms for problems in the field of geodesy.

About the project

Cluster of Excellence: Hausdorff Center for Mathematics (HCM)

At HCM, we work with colleagues from discrete mathematics on fundamental questions in the field of algorithms and complexity.

About the Cluster of Excellence

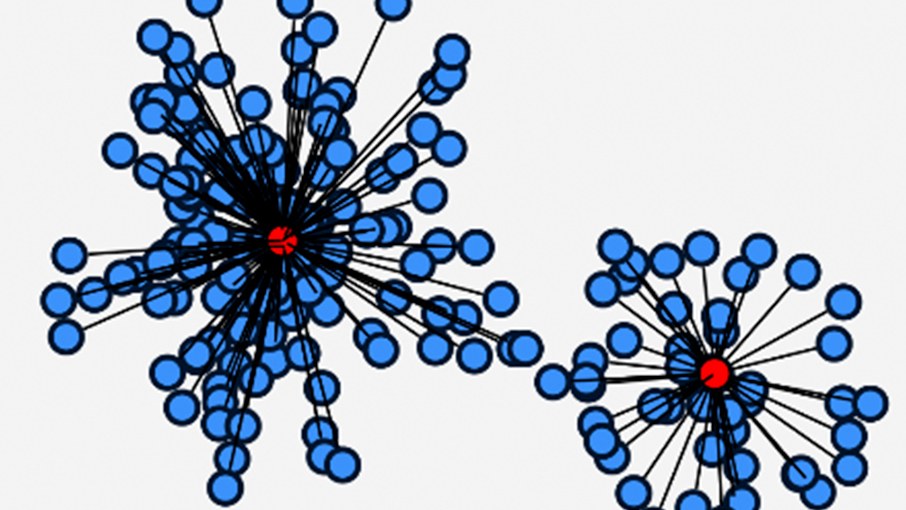
DFG grant: Theoretical Investigation of Practical Issues in Cluster Analysis

In this project, new algorithms in the area of hierarchical clustering and clustering with constraints were designed.

About the project

New Edition of the German Textbook "Algorithmische Geometrie"

The new edition of the German textbook "Algorithmische Geometrie" by Rolf Klein, Anne Driemel and Herman Haverkort has been published.

To the publication

DFG grant: Understanding Posted Prices Through Prophet Inequalities

In this project, we are developing a better understanding of how complex prices need to be in scenarios with multiple goods.

About the project

Working Groups

The department consists of three working groups: Prof. Dr. Anne Driemel and her research group represent the field of "Algorithmic Geometry". Algorithmic Geometry is a subfield of algorithmics with strong links to discrete geometry and combinatorics. Algorithmic techniques from this field enable the efficient solution of complex geometric problems, which leads to advanced technologies in scientific applications and in industry.

The working group of Prof. Dr. Thomas Kesselheim deals with "Algorithmic Game Theory and Optimization Under Uncertainty". Many typical application scenarios of algorithms deviate from the classical scheme that an output must be calculated for a given input: Not all information is known in advance or algorithms interact with agents that maximize their own utility. With the help of a better understanding of the possibilities and limitations, we develop new algorithms for various applications, especially for electronic markets.

Prof. Dr. Heiko Röglin's research group focuses on the "Analysis of Algorithms Beyond the Worst Case and Algorithms for Cluster Analysis". The aim of analyzing algorithms beyond the worst case is to gain a better understanding of the algorithms and to rigorously explain experimental observations. This provides new insights that help in the design of better algorithms. Cluster analysis is an important problem in the field of data analysis that plays a major role in numerous applications. In this area, we develop new algorithms and models with the aim of improving the state of the art.